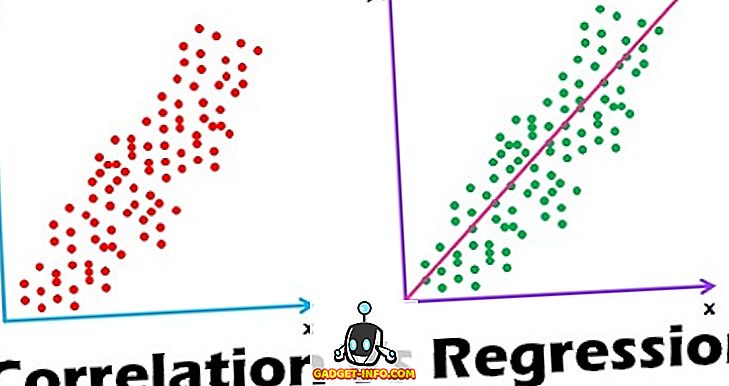
A korreláció és a regresszió közötti különbség az interjúk egyik leggyakrabban feltett kérdése. Ráadásul sokan kétértelműen érzik magukat a kettő megértésében. Tehát teljes körűen olvassa el ezt a cikket, hogy egyértelműen megértse ezeket a kettőt.
Összehasonlító táblázat
| Az összehasonlítás alapja | Korreláció | Regresszió |
|---|---|---|
| Jelentés | A korreláció egy statisztikai mérés, amely meghatározza a két változó társulását vagy társítását. | A regresszió leírja, hogy egy független változó számszerűen kapcsolódik-e a függő változóhoz. |
| Használat | Két változó közötti lineáris kapcsolat ábrázolása. | A legjobb vonal és egy változó becslése egy másik változó alapján. |
| Függő és független változók | Semmi különbség | Mindkét változó eltérő. |
| Azt jelzi | A korrelációs együttható jelzi, hogy a két változó milyen mértékben mozog együtt. | A regresszió jelzi az egység változásának hatását a becsült változó (y) ismert változójában (y). |
| Célkitűzés | A változók közötti kapcsolatot kifejező numerikus érték keresése. | A véletlen változó értékeinek meghatározása a fix változó értékei alapján. |
A korreláció meghatározása
A „korreláció” kifejezés két szó kombinációja (együtt) és két mennyiség közötti kapcsolat (kapcsolat). A korreláció akkor következik be, amikor két változó vizsgálatakor megfigyelhető, hogy egy változó egységváltozása egy másik változó egyenértékű változásával, azaz közvetlen vagy közvetett változással történik. Vagy egyébként a változók nem korreláltak, ha az egyik változóban való mozgás nem egy másik változóban meghatározott irányú mozgást jelent. Ez egy statisztikai technika, amely a változók párja közötti kapcsolat erősségét képviseli.
A korreláció pozitív vagy negatív lehet. Amikor a két változó ugyanabban az irányban mozog, azaz egy változó növekedése egy másik változó megfelelő növekedését eredményezi, és fordítva, akkor a változók pozitív korrelációnak tekinthetők. Például : nyereség és befektetés.
Éppen ellenkezőleg, ha a két változó különböző irányban mozog, oly módon, hogy egy változó növekedése egy másik változó csökkenését eredményezi, és fordítva, ez a helyzet negatív korreláció néven ismert. Például : Egy termék ára és igénye.
A korrelációs intézkedéseket az alábbiak szerint adjuk meg:
- Karl Pearson termék-pillanat korrelációs együtthatója
- Spearman rangkorrelációs együtthatója
- Szórási diagram
- Az egyidejű eltérések együtthatója
A regresszió meghatározása
A két vagy több változó átlag matematikai kapcsolatának függvényében egy vagy több független változóban bekövetkezett változás miatt a metrikus függő változó változásának becslésére szolgáló statisztikai technikát regressziónak nevezzük. Jelentős szerepet játszik számos emberi tevékenységben, mivel ez egy erőteljes és rugalmas eszköz, amely a múltbeli, jelenlegi vagy jövőbeli események előrejelzésére szolgál a múltbeli vagy jelen események alapján. Például : A múltbeli rekordok alapján egy vállalkozás jövőbeni nyeresége becsülhető.
Egy egyszerű lineáris regresszióban két x és y változó van, ahol y függ az x-től vagy az x által befolyásoltól. Itt y-t függőnek, vagy kritériumváltozót és x független vagy előrejelző változót nevezünk. Az y x regressziós sora az alábbiak szerint van kifejezve:
y = a + bx
ahol a = állandó,
b = regressziós együttható,
Ebben az egyenletben a és b a két regressziós paraméter.
A korreláció és a regresszió közötti különbségek
Az alábbiakban megadott pontok részletesen ismertetik a korreláció és a regresszió közötti különbséget:
- A statisztikai mérés, amely meghatározza a két mennyiség együttm ködését vagy társítását, Korreláció néven ismert. A regresszió leírja, hogy egy független változó számszerűen kapcsolódik-e a függő változóhoz.
- A korrelációt két változó közötti lineáris kapcsolat reprezentálására használjuk. Éppen ellenkezőleg, a regressziót arra használják, hogy illeszkedjen a legjobb vonalhoz, és egy változót egy másik változó alapján becsüljünk.
- A korrelációban nincs különbség a függő és független változók között, azaz az x és y közötti korreláció hasonló az y és x értékekhez. Ezzel ellentétben az y x-en lévő regressziója különbözik az y-ről.
- A korreláció a változók közötti kapcsolat erősségét jelzi. Ellentétben a regresszió tükrözi az egység változásának hatását a független változóban a függő változóra.
- A korreláció célja egy olyan numerikus érték megtalálása, amely a változók közötti kapcsolatot fejezi ki. A regressziótól eltérően, amelynek célja a véletlen változó értékeinek előrejelzése a fix változó értékei alapján.
Következtetés
A fenti vitával nyilvánvaló, hogy nagy különbség van a két matematikai fogalom között, bár ezek a kettő együtt tanulmányozva. A korrelációt akkor használják, ha a kutató azt akarja tudni, hogy a vizsgált változók korreláltak-e vagy sem, ha igen, akkor mi az egyesület ereje. Pearson-féle korrelációs együtthatót a korreláció legjobb mértékének tekintjük. A regresszióanalízis során két változó közötti funkcionális kapcsolatot alakítunk ki az események jövőbeli előrejelzése érdekében.