
Eltérően, a szórás a variancia kiszámításakor kapott számérték értékének négyzetgyöke. Sokan ellentétesek a két matematikai koncepcióval. Tehát ez a cikk megpróbálja megvilágítani a szórást és a szórást.
Összehasonlító táblázat
| Az összehasonlítás alapja | Variancia | Standard eltérés |
|---|---|---|
| Jelentés | A variancia egy numerikus érték, amely a megfigyelések aritmetikai átlagától való változékonyságát írja le. | A standard eltérés a mérések egy adatcsoporton belüli szétszóródásának mértéke. |
| Mi az? | Ez a négyzetes eltérések átlaga. | Ez a négyzet eltérése. |
| Címkézve: | Sigma-négyzet (σ ^ 2) | Sigma (σ) |
| Valamiben kifejezve | Négyzetes egységek | Ugyanazok az egységek, mint az adatsor értékei. |
| Azt jelzi | Mennyire terjednek el egy csoportban lévő egyének. | Mennyire különbözik az adatállomány megfigyelése az átlagtól. |
A variancia meghatározása
A statisztikában a variancia a változékonyság mértéke, amely azt mutatja, hogy egy csoport tagjai mennyire terjednek el. Megállapítja, hogy az átlagos megfigyelés milyen mértékben változik az átlagtól. Ha egy adatkészlet varianciája kicsi, az az adatok pontosságát mutatja az átlaghoz viszonyítva, míg a nagyobb varianciaérték azt mutatja, hogy a megfigyelések nagyon szét vannak szórva az aritmetikai átlag és egymástól.
Nem minősített adatok esetén :
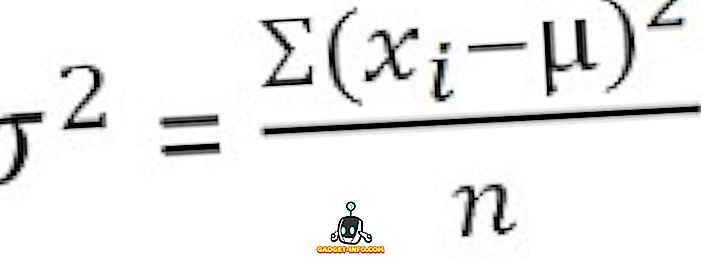
Csoportosított frekvenciaelosztás esetén :
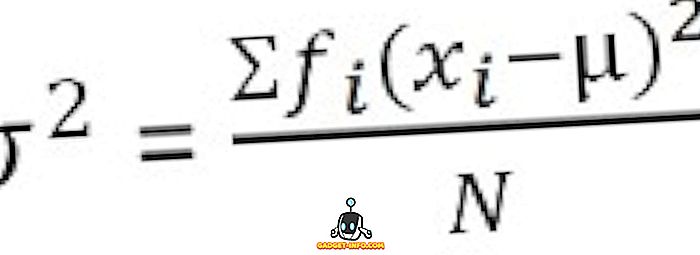
A standard eltérés meghatározása
A standard eltérés egy olyan intézkedés, amely számszerűsíti a megfigyelések diszperziójának mennyiségét egy adatállományban. Az alacsony szórás a mutatószámok aritmetikai átlaghoz való közelségének és a magas szórásnak a mutatója; a pontszámok nagyobb értékek között oszlanak el.
Nem minősített adatok esetén :

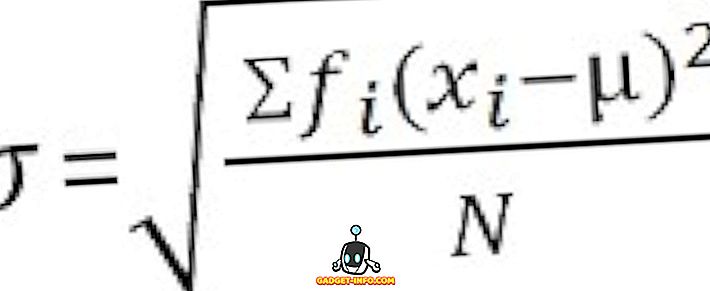
A variancia és a standard eltérés közötti különbségek
A szórás és a szórás közötti különbség egyértelműen a következő okokból vonható le:
- A variancia egy numerikus érték, amely a megfigyelések aritmetikai átlagától való változékonyságát írja le. A standard eltérés a mérések egy adatcsoporton belüli szétszóródásának mértéke.
- A variancia nem más, mint egy négyzetes eltérés. Másrészről a standard eltérés a négyzet négyzetes eltérése.
- A varianciát sigma-négyzet (σ2) jelöli, míg a szórás sigma (σ).
- A varianciát négyzetegységekben fejezzük ki, amelyek általában nagyobbak, mint az adott adatkészlet értékei. A standard eltéréssel ellentétben, amelyet ugyanazokban az egységekben fejeznek ki, mint az adatkészlet értékei.
- A variancia azt méri, hogy a csoportban lévő egyének mennyire terjednek ki. Ezzel szemben a standard deviáció azt méri, hogy az adatkészletek mennyire különböznek az átlagtól.
Ábra
A diákok által öt tárgyban szerzett jelek 60, 75, 46, 58 és 80 fő. Meg kell találnod a szórást és a szórást.
Először is, meg kell találnod az átlagot,

Így az átlagos (átlag) jelek 63, 8
Most kiszámolja a varianciát
| x | A | (Xa) | (XA) ^ 2 |
|---|---|---|---|
| 60 | 63, 8 | -3.8 | 14.44 |
| 75 | 63, 8 | 11.2 | 125, 44 |
| 46 | 63, 8 | -17, 8 | 316, 84 |
| 58 | 63, 8 | 5.8 | 33.64 |
| 80 | 63, 8 | 16.2 | 262, 44 |
Hol, X = megfigyelések
A = számtani átlag
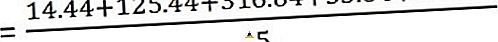
És a standard eltérés -

Hasonlóságok
- Mind a szórás, mind a szórás mindig pozitív.
- Ha az adatállomány összes megfigyelése azonos, akkor a szórás és a szórás nulla lesz.
Következtetés
Ez a két alapvető statisztikai kifejezés, amely létfontosságú szerepet játszik a különböző ágazatokban. A standard szórás az átlagnál előnyösebb, mivel ugyanazokban az egységekben fejezzük ki, mint a mérések, míg a variancia az adott adathalmaznál nagyobb egységekben van kifejezve.









