A rendezés egy alapművelet, amelyben a tömb elemeit egy bizonyos sorrendben rendezik annak érdekében, hogy megkönnyítsék a kereshetőséget. Egyszerű szavakkal az adatok rendezése úgy történik, hogy könnyen megkereshető legyen.
Összehasonlító táblázat
| Az összehasonlítás alapja | Beillesztés Rendezés | Kiválasztás Rendezés |
|---|---|---|
| Alapvető | Az adatokat az adatok egy meglévő rendezett fájlba való beillesztésével rendezik. | Az adatokat az egymást követő elemek válogatott helyre történő kiválasztásával és elhelyezésével rendezik. |
| Természet | Stabil | Instabil |
| A követendő folyamat | Az elemek már ismertek, míg az elhelyezés helyét keresik. | A hely korábban ismert, míg az elemeket keresik. |
| Azonnali adatok | A beillesztési sorrend az élő válogatási technika, amely azonnali adatokkal foglalkozik. | Nem tud azonnal kezelni az adatokat, az elején jelen kell lennie. |
| A legjobb eset komplexitás | Tovább) | O (n 2 ) |
A beszúrás rendezése
A beszúrási rendezés az értékek halmazának beillesztésével a meglévő rendezett fájlba kerül. A rendezett tömböt egyszerre egyetlen elem beillesztésével állítja össze. Ez a folyamat addig folytatódik, amíg az egész tömböt sorrendben rendezik. A beillesztés sorrendjében az elsődleges koncepció az, hogy minden elemet a megfelelő listába helyezzen. A beillesztési módszer hatékony memóriát takarít meg.
A beszúrás rendezése
- Két tömbkészletet használ, amelyekben a rendezett adatokat és a nem rendezett adatokat tárolja.
- A rendezési algoritmus mindaddig működik, amíg el nem látnak elemeket a nem rendezett készletben.
- Tételezzük fel, hogy a tömbben „n” számú elem található. Kezdetben a 0-as indexű elem (LB = 0) létezik a rendezett készletben. A fennmaradó elemek a lista rendezetlen partíciójában vannak.
- A nem válogatott rész első eleme 1 tömb index (ha LB = 0).
- Minden egyes iteráció után kiválasztja a nem rendezett partíció első elemét, és beilleszti azt a rendezett helyre a megfelelő helyre.
A beillesztés előnyei
- Könnyen végrehajtható és nagyon hatékony, ha kis adatállományokkal használjuk.
- A beillesztési fajta további memóriaterülete kisebb (azaz O (1)).
- Élő rendezési technikának tekintendő, mivel a listát az új elemek fogadásakor rendezheti.
- Gyorsabb, mint más rendezési algoritmusok.
Példa :
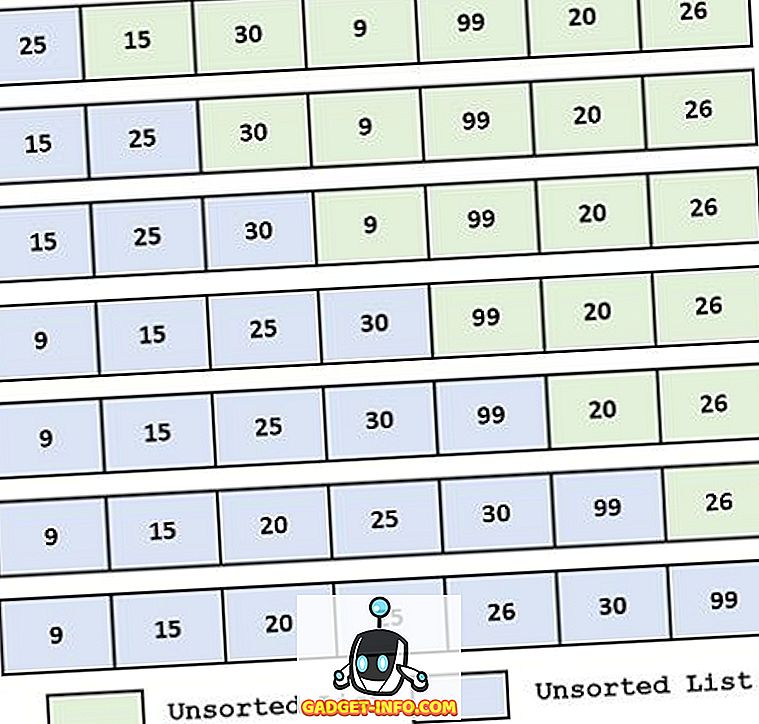
A kiválasztás meghatározása Rendezés
A Kiválasztás rendezi a válogatást a minimális érték számának megkeresésével és az első vagy utolsó pozícióba rendezésével (növekvő vagy csökkenő). A minimális kulcs keresésének és a megfelelő pozícióba helyezésének folyamatát addig folytatjuk, amíg az összes elem helyes helyzetbe kerül.
A kiválasztás kezelése Rendezés
- Tegyük fel, hogy egy ARR tömb N-eleme van a memóriában.
- Az első lépésben a legkisebb kulcsot a pozíciójával együtt keresik, majd az ARR [POS] az ARR-vel [0] cserélhető. Ezért az ARR [0] rendezésre kerül.
- A második lépésben a legkisebb érték pozícióját az N-1 elemek alcsoportjában határozzuk meg. Cserélje ki az ARR-t [POS] az ARR-vel [1].
- Az N-1 lépésben ugyanazt a folyamatot hajtjuk végre az N számú elem rendezésére.
Példa :
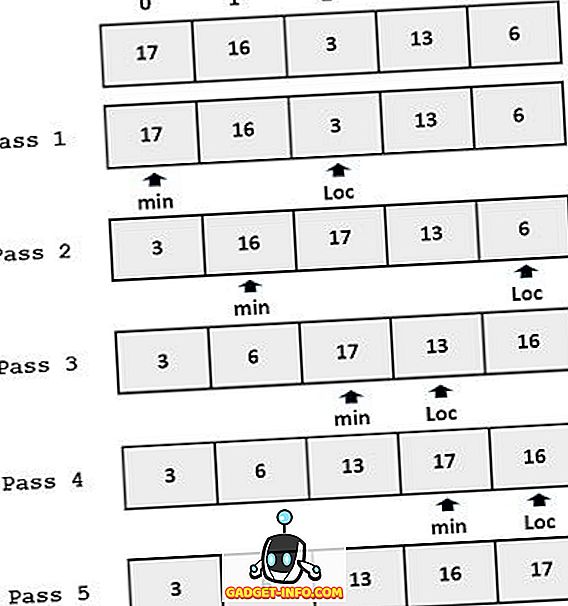
A beillesztés és a kiválasztás közötti különbségek sorrendje
- A beillesztési sorrend általában végrehajtja a beszúrási műveletet. Éppen ellenkezőleg, a szelekciós sort a szükséges elemek kiválasztását és elhelyezését végzi.
- A beillesztési sort stabilnak tartják, míg a szelekciós rendezés nem stabil algoritmus.
- A beillesztési rendezési algoritmusban az elemek korábban ismertek. Ezzel szemben a kiválasztási sorrend előzőleg tartalmazza a helyet.
- A beillesztési rend egy élő válogatási technika, ahol a beérkező elemek azonnal sorrendbe kerülnek a listában, míg a kiválasztási rendezés nem működik jól azonnali adatokkal.
- A beillesztési rendnek a legjobb esetben O (n) futási ideje van. Ezzel ellentétben a kiválasztási típus legjobb esettanulmányi komplexitása O (n2).
A beillesztés összetettsége
A beillesztés rendezésének legjobb esete az O (n) idők, azaz amikor a tömb korábban rendezve van. Ugyanígy, ha a tömböt fordított sorrendben rendezzük, a nem rendezett tömb első elemét össze kell hasonlítani a rendezett készlet minden egyes elemével. Tehát a legrosszabb esetben az Insertion sort futási ideje kvadratikus, azaz O (n2) . Átlagos esetben a minimális (k-1) / 2 összehasonlításra is szükség van. Ezért az átlagos esetnek az O (n2) kvadratikus futási ideje is van.
A kiválasztás összetettsége
Mivel a kiválasztás, a rendezés nem függ a tömb elemeinek eredeti sorrendjétől, ezért nincs sok különbség a legjobb eset és a legrosszabb esetkomplexitás között.
A kiválasztási sort kiválasztja a minimális érték elemet, a kiválasztási folyamatban az összes 'n' elemszámot beolvassa; ezért az első lépésben n-1 összehasonlítás történik. Ezután az elemeket kicseréljük. A második lépésben a második legkisebb elem megtalálásához hasonlóan a többi n-1 elem szkennelését igényeljük, és a folyamatot egész sorrendig folytatjuk.
Így a kiválasztási típus futási idejének összetettsége O (n2) .
= (n-1) + (n-2) + ……… .. + 2 + 1
= n (n-1) / 2 = O (n2)
Következtetés
Mindkét rendezési algoritmus közül a beillesztési rendezés gyors, hatékony, stabil, míg a szelekciós rendezés csak akkor működik hatékonyan, ha a kis elemkészlet részt vesz, vagy a lista részben válogatott. A szelekciós rendezéssel végzett összehasonlítások száma nagyobb, mint a végrehajtott mozgások, míg a beillesztésnél az elem mozgatásának vagy cseréjének száma nagyobb, mint az összehasonlítás.