A központi tendencia ideális mérőeszköze egyértelműen meghatározható, könnyen érthető, egyszerűen kiszámítható. Ennek az összes megfigyelésen kell alapulnia, és legkevésbé az adatkészletben levő szélsőséges megfigyelések által.
Az emberek gyakran ellentétben állnak a két intézkedéssel, de az a tény, hogy különböznek egymástól. Ez a cikk kifejezetten kiemeli az átlag és a medián közötti alapvető különbségeket. Nézd meg.
Összehasonlító táblázat
| Az összehasonlítás alapja | Átlagos | Középső |
|---|---|---|
| Jelentés | Az átlag az adott értékek vagy mennyiségek egyszerű átlagára utal. | A medián a rendezett értékek listájában a középső szám. |
| Mi az? | Ez számtani átlag. | Pozitív átlag. |
| jelentése | Az adatkészlet súlypontja | Az adatkészlet súlypontja Az adatkészlet középpontja |
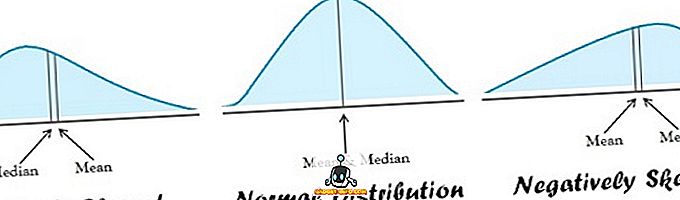
| Alkalmazhatóság | Normális eloszlás | Döntött eloszlás |
| A kiugró | Az átlag érzékeny a kiugró értékekre. | A medián nem érzékeny a kiugró értékekre. |
| Számítás | Az átlagot az összes megfigyelés összeadásával számítjuk ki, majd a kapott értéket megosztjuk a megfigyelések számával. | A medián kiszámításához az adatkészlet növekvő vagy csökkenő sorrendben van elrendezve, majd az új adatsor közepére eső érték medián. |
Az átlag meghatározása
Az átlag a központi tendencia széles körben alkalmazott mértéke, amely az értékek halmazának átlagaként definiált. Ez képviseli az adott értéktartomány modelljét és leggyakoribb értékét. Mind a diszkrét, mind a folytonos sorozatokban kiszámítható.
Az átlag egyenlő az összes megfigyelés összegével, és az adatokban lévő megfigyelések számával. Ha a változó által feltételezett érték egyenlő, akkor átlagértéke is azonos lesz. Az átlag kétféle lehet, a minta átlaga (x̅) és a populáció átlaga (µ). Kiszámítható adott képlettel:
- A számtani átlag :

n = az értékek száma - Diszkrét sorozathoz :

- Folyamatos kiszolgálás esetén :

A = feltételezett átlag
C = Közös osztó
A medián meghatározása
A medián a központi tendencia egy másik fontos mérőeszköze, amelyet az érték két egyenlő részre osztására használnak, azaz a minta, a populáció vagy a valószínűség eloszlásának nagyobb felét az alsó feléből. Ez a középső érték, amely akkor érhető el, ha a megfigyelések meghatározott sorrendben, növekvő vagy csökkenő sorrendben vannak rendezve.
A medián kiszámításához először a legkisebb és a legmagasabb, illetve a legalacsonyabb értékre kell állítani a megfigyeléseket, majd az alábbi feltételek szerint alkalmazza a megfelelő képletet:
- Ha a megfigyelések száma páratlan :

- Ha a megfigyelések száma még :

- Folyamatos sorozat :

c = az előző medián osztály kumulatív gyakorisága
f = a medián osztály gyakorisága
h = osztályszélesség
Az átlag és a medián közötti különbségek
Az átlag és a medián közötti jelentős különbségeket az alábbi cikk tartalmazza:
- A statisztikákban az átlag az adott értékek vagy mennyiségek egyszerű átlaga. A medián a rendezett értékek listájában a középső szám.
- Míg az átlag az aritmetikai átlag, a medián pozicionális átlag, lényegében az adathalmaz helyzete határozza meg a medián értékét.
- Az átlag felvázolja az adatkészlet súlypontját, míg a medián kiemeli az adatkészlet középértékét.
- Az átlag megfelel a normálisan elosztott adatoknak. A másik végén a medián a legjobb, ha az adateloszlás ferde.
- Az átlagot nagymértékben befolyásolja az a szélsőséges érték, amely nem a mediánnál van.
- Az átlagot az összes megfigyelés összeadásával számítjuk ki, majd a kapott értéket osztjuk a megfigyelések számával; az eredmény átlag. A mediánnal ellentétben az adatkészlet növekvő vagy csökkenő sorrendben van elrendezve, majd az új adatkészlet közepére eső érték medián.
Példa
Keresse meg az adott adathalmaz átlagát és mediánját:
58, 26, 65, 34, 78, 44, 96
Megoldás: Az átlag kiszámításához meg kell osztani a megfigyelések összegét a megfigyelések számával,

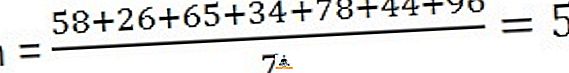
A medián kiszámításához először a sorozatot rendezze el, azaz a legalacsonyabb és a legmagasabb érték között.
26, 34, 44, 58, 65, 78, 96
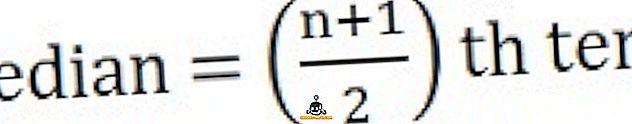
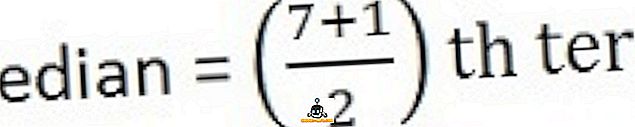
Következtetés
A fenti pontok áttekintése után elmondhatjuk, hogy ezek a két matematikai koncepció különbözik. Az aritmetikai átlagot vagy az átlagot a központi tendencia legjobb mérőszámának tekintik, mivel az ideális intézkedés valamennyi jellemzőjét tartalmazza, de hátránya, hogy a mintavételi ingadozások befolyásolják az átlagot.
Hasonlóképpen, a medián egyértelműen meghatározható és könnyen érthető és kiszámítható, és a legjobb dolog az, hogy a mintavétel ingadozásai nem befolyásolják, de a medián egyetlen hátránya az, hogy nem mindenre épül. megfigyelések. Nyitott végosztályozás esetén a medián általában az átlagnál előnyösebb.